Password cracking is one of those topics that might look like a shallow puddle at first—but step in, and you’ll quickly realize it can swallow you whole. To make sense of the more advanced tools and techniques I’ll cover later, we first need to break down the fundamentals: how passwords are stored, how they’re protected, and the strategies used to crack them. Without that foundation, the advanced material won’t stick.
This post is the groundwork—the reference material I’ll be pointing back to in future write-ups. If you’re already comfortable with the basics, think of this as a solid refresher or something to share with folks who are just getting started. If you’re brand new, you’re in the right place. We’re starting from absolute zero.
Note to Developer; Use Argon2id
Before we dive in, a quick note on hashing algorithms. Throughout this post, I’ll be referencing a variety of hash functions, along with their strengths and weaknesses. Just to be clear—I’m discussing these algorithms strictly in the context of password cracking and defense analysis.
If you’re a developer looking for the best algorithm to store passwords securely, let me save you some time: this is a solved problem. Use Argon2id. Full stop.
That said, I know not every environment supports Argon2 just yet. If you’re in that boat, your next best option is Scrypt. If neither Argon2id nor Scrypt are supported, then your last strong option is to use Bcrypt. It’s not cutting-edge, but it’s still a solid, battle-tested choice.
Hashing; The What & Why
This post won’t dive into the math behind hashing—that’s been covered elsewhere, and I am not that smart… Instead, I’ll highlight a few core concepts needed for context.
Why do we have hashes?
Storing plaintext passwords is insecure, yet some applications still do it. The correct approach is to hash passwords before storing them. When a user sets a password, it’s hashed and stored. During login, the input is hashed again and compared to the stored hash. If they match, access is granted.
This is the basic mechanism behind secure password verification.
What is a “hash”? Also, De-hashing is NOT a Thing…

A hash is a one-way cryptographic function—one-way being the key term here. This means that once data is processed through a hash function, there’s no feasible method to reverse the process and retrieve the original input.
A hash function takes input data and produces a fixed-length cryptographic digest (the “hash”) that is deterministically correlated to that input. You can hash anything: a single word, an entire paragraph, or even the full text of a book. Regardless of the input size, the output will always be the same fixed length, depending on the hashing algorithm used.
For example, if you hash the full contents of a novel using MD5, you’ll get a 32-character hash. Hash a single word using the same algorithm? Still 32 characters. This property underscores the impossibility of reversing a hash—there’s simply no way to derive the original input from a 32-character output.
Hashing is not Encryption
By now, we understand that hashing is the process of taking input data and deterministically producing a randomized-looking output. This output, known as a hash, is one-way—meaning it cannot be reversed to reveal the original plaintext data.
In contrast, encryption transforms data into a scrambled format that appears random but is designed to be reversible. With the correct decryption key, the encrypted data can be converted back into its original plaintext form.
As you can see, hashing and encryption serve very different purposes in cryptography. Hashing is ideal for integrity checks and password storage, where reversibility is undesirable. Encryption, on the other hand, is used to protect the confidentiality of data during storage or transmission.
How do we crack a hash?
So, we now know that you cannot decrypt, de-hash, or reverse a hash. In order to “crack” a password hash we perform the following process.
- Guess a plaintext password.
- Send the plaintext password into the hashing algorithm function.
- Check if the guessed hashed plaintext password output matches the hash we are trying to crack.
- If they match, then we cracked the password.
- If they do not match, make a new password guess.
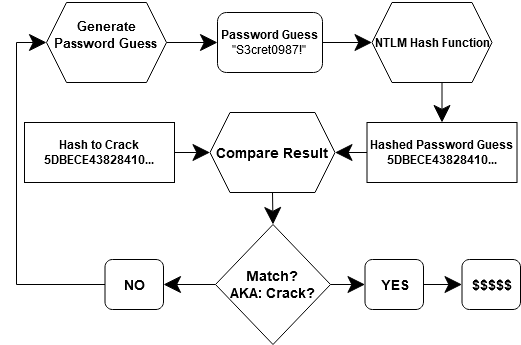
If a plaintext password and its resulting hash match the hash we are trying to crack, then we have cracked the password. Frankly, I am not sure why we call it “cracking.” It’s really guessing and checking, but I suppose “password guess & check” doesn’t sound as cool as “password cracking.”
Section Key Terms
Hash == A fixed-size, deterministically correlated result of data passed into a one-way cryptographic function. A hash cannot be reversed to retrieve the original input. Hashes are also commonly referred to as digests.
PlainText Password == A password in its original, human-readable form before any cryptographic processing, such as hashing or encryption.
Hashing Algorithm == A deterministic function that converts input data—such as a plaintext password—into a fixed-length hash. Different algorithms (e.g., MD5, SHA-256, bcrypt) produce different hash lengths and offer varying levels of security.
One-Way Function == A cryptographic process designed so that its output cannot be feasibly reversed to reveal the original input. Hashing is a prime example of a one-way function.
Password Cracking == The process of attempting to recover a plaintext password by guessing potential passwords, hashing each guess, and comparing the resulting hashes against a stored hash until a match is found.
Hashing Algorithms
There are many different types of hashing algorithms, each designed with specific use cases and security considerations in mind. Some hashing algorithms function as cryptographic primitives, while others are constructed by combining multiple primitives to achieve enhanced security or functionality.
Cryptographic primitives are the most fundamental and stripped-down implementations of hashing algorithms. They form the building blocks for more complex cryptographic systems. Examples of well-known cryptographic hash primitives include MD5, SHA-1, SHA-512, and RIPEMD-160.
Combining Cryptographic Primitives in Hashing Algorithms
Cryptographic primitives can be combined to form layered hashing algorithms, often with the goal of increasing complexity or obfuscating patterns.
Let’s break down an example:
Input Plaintext Password: password
Hashing Algorithm: MD5(SHA1(password))
This method first hashes the password using the SHA-1 algorithm, then takes that output and passes it through the MD5 algorithm. Here’s what that process looks like step by step:
Phase 1: SHA-1
We start by hashing the plaintext password using SHA-1:
SHA1(“password”) = 5baa61e4c9b93f3f0682250b6cf8331b7ee68fd8
This produces a 40-character hexadecimal digest.
Phase 2: MD5
Next, we take the SHA-1 hash output and feed it into the MD5 function:
MD5(“5baa61e4c9b93f3f0682250b6cf8331b7ee68fd8”) = 87edf916ddf0d403ea3d5e3c587e2d8c
The result is a 32-character MD5 hash. At this point, the original password has been transformed through two cryptographic layers.
You can take any number of hashing primitives to make new hashing algorithms.
Section Key Terms
Hashing Primitives == low-level, well-defined cryptographic functions—such as SHA-256 or MD5—that take input data and deterministically produce a fixed-size, pseudorandom output used as the foundation for higher-level security protocols.
Salting & Peppering in Hash Algorithms
Salting and peppering are techniques used to enhance the security of password hashes by introducing additional data into the hashing process. Both methods involve adding a string(or any data) into the hashing algorithm, but they differ in how this string is managed outside of the hashing algorithm.
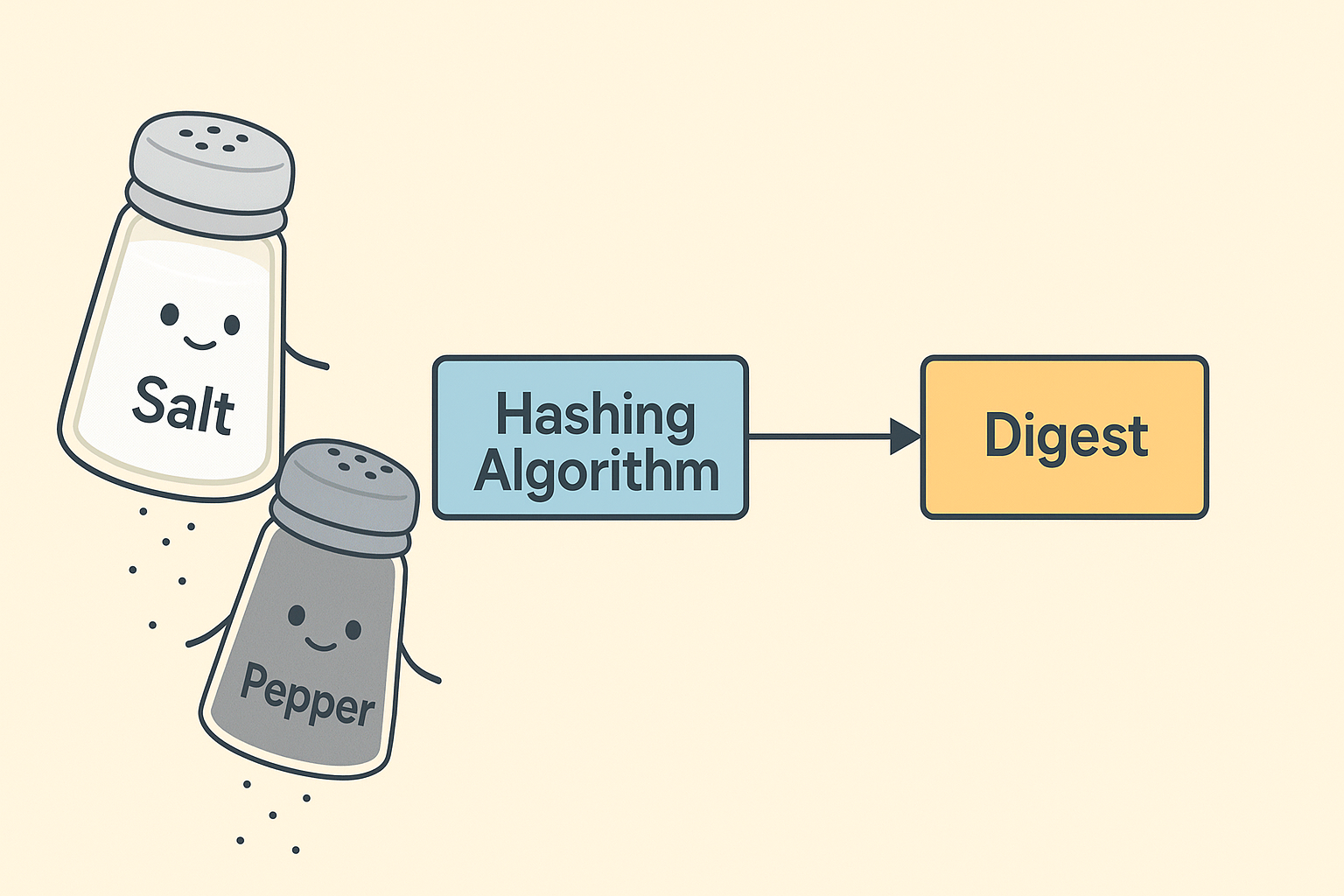
To clarify the distinction, consider a website with multiple user accounts. When salting is used, each user’s password is combined with a unique, randomly generated string—known as a salt—before hashing. This ensures that even if two users have the same password, their resulting hashes will be different.
In contrast, peppering involves using a single, secret string—called a pepper—that is applied to all user passwords before hashing. Unlike salts, peppers are typically kept secret and stored separately from the password database. If a site is peppering passwords, every account shares the same additional string in the hashing process.
Why don’t I see any hashing algorithms using a pepper?
To the hashing algorithm itself, there is no inherent distinction between a salt or a pepper. Both are simply additional pieces of data that are combined with the input (typically a password) before the hash is generated. The algorithm processes this combined input the same way, regardless of whether the extra data is unique per user (salt) or shared across all users (pepper).
For this reason, you will see many Wiki pages and discussions that never mention anything about peppers and only discuss salts, but that extra input could be either.
How are Salts or Peppers Applied?
Expanding upon our hashing algorithm discussion, let’s now introduce salting into the equation. A common implementation can be seen in the SHA-256-based algorithm used in Hashcat hash-mode 1410, which is expressed as sha256($pass.$salt).
A Simple Use of a Salt
In this method, the plaintext password and the plaintext salt are concatenated before being passed into the SHA-256 hashing function.
$pass = 5ecr3t
$salt = 8675309
Algorithm = sha256($pass.$salt)
Result: sha256($pass.$salt)
sha256(5ecr3t8675309) = 9b77d226257194ecf7d6a1f7e1bee8ac1f3b9893ec13bb0bba8942377b64a6c4
Even though the sha256($pass.$salt) algorithm uses a salt, it’s still possible to reproduce the same hash and crack the password—if you correctly guess "5ecr3t8675309" as the password.
A More Complex Use of a Salt
To mitigate the risk of accidentally guessing salted passwords(especially in cases where salts are predictable or known), an additional layer of complexity can be introduced by hashing the password and the salt separately before combining them. A practical example of this approach is the algorithm md5(md5($pass).md5($salt)), used in Hashcat mode 3910.
Lets break down this example.
$pass = 5ecr3t
$salt = 8675309
Algorithm = md5(md5($pass).md5($salt))
Phase 1: md5($pass).md5($salt)
md5($pass).md5($salt)md5(5ecr3t)md5(675309)
Phase 2: md5(<Phase1Result>)
md5(<Phase1Result>)md5(897788fae67e978a393acdb97a2312036cc0d36686e6a433aa76f96773852d35)
Result:
md5(md5(5ecr3t).md5(675309)) = 45f617b94a7fd6bc6c997ad36f2a3c14
In this scheme, the password and salt are each hashed with MD5, then their digests are concatenated and hashed again. This adds complexity, forcing us to account for intermediate hashes rather than just combining plaintexts.
A final thought on algorithms like the one above: for decades, web and software developers have devised countless hashing algorithms that rely on obscurity rather than sound cryptographic principles. While I’ve highlighted security improvements between certain algorithms, none of the ones discussed should be considered secure for real-world use. As mentioned at the beginning of this post, refer to vetted, industry-standard cryptographic functions when designing secure systems.
Why Peppers Alone are Weak
One way to determine whether a set of password hashes was salted or peppered is by analyzing the presence of duplicate hashes in the database. In any sufficiently large user base, it’s statistically likely that multiple users will choose the same plaintext password.
If no salting is used (or if peppering alone is applied), identical plaintext passwords will produce identical hashes. As a result, you’ll observe repeated hash values throughout the database.
However, when proper salting is implemented, each user’s password is combined with a unique salt before being hashed. Even if two users select the same password, their individual salts will cause the resulting hashes to differ. In such a case, you should not see any duplicate hash values in the dataset, assuming a properly implemented and randomized salting process.
Section Key Terms
Salt == A unique, randomly generated string added to each password before hashing. It ensures that identical passwords result in different hashes, preventing attackers from using precomputed tables (like rainbow tables) to crack hashes.
Pepper == A secret value shared across all user passwords, added during hashing. Unlike salts, peppers are not stored alongside the hashes and are kept confidential, often within application code or hardware security modules.
Concatenation == The process of joining two strings end-to-end. In hashing, this often refers to joining the password with a salt or pepper before passing it into the hashing function. Concatenation is used anywhere in the hashing algorithm where you see a "." as in sha256($pass.$salt).
Hash Modes == Specific hash algorithm identifiers used in Hashcat. For instance, mode 1410 represents sha256($pass.$salt), and mode 3910 represents md5(md5($pass).md5($salt)).
Duplicate Hashes == Identical hash outputs that suggest users may have used the same password. Their presence in a database can indicate the absence of proper salting.
Intermediate Hashes == Hashes generated during multi-phase hashing processes, often used to increase computational complexity and defense against brute-force attacks.
Hash Iterations and Cost
When we talk about “iterations” in password hashing, we’re referring to how many times the hashing algorithm runs over the input. Instead of hashing a password once and calling it a day, we deliberately hash it hundreds or thousands of times. This slows things down in a good way for security, a bad way if you are a password cracker. It makes password cracking exponentially more expensive.
More iterations = more work = harder cracking
Let’s take the most basic example of hash iteration. Say we’re using MD5 with an iteration count of two. That would look like this: MD5(MD5(password))
The output of the first MD5 hash is fed into the second iteration. In effect, we’ve doubled the amount of work required to compute the final hash.
To expand upon this idea, let’s take a look at a snippet of code from the phpass codebase.
if (PHP_VERSION >= '5') {
$hash = md5($salt . $password);
do {
$hash = md5($hash . $password);
} while (--$count);
}In the above snippet of code we can see that the hash output is iterated over many times. See the flow diagram below.
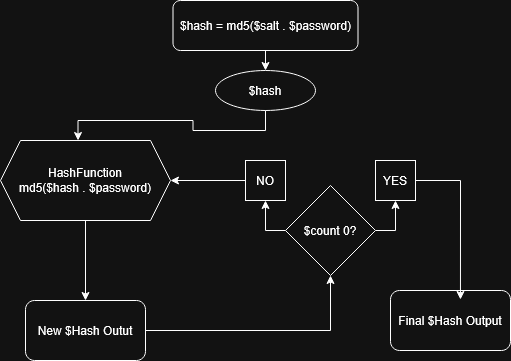
The iteration count is also referred to as the “rounds” depending on the context. In the examples I provided earlier, the iteration count is applied in a straightforward, linear manner.
Cost Factor
A cost factor in a hashing algorithm is conceptually similar to an iteration count, but it’s applied differently. Rather than being used in a linear fashion—where the number directly indicates how many times the function runs—the cost factor is typically applied exponentially.
For example, in bcrypt, the cost factor determines the number of hashing rounds by using it as the exponent of two. So, a cost factor of 12 results in 2¹², or 4,096 rounds.
Section Key Terms
Iteration Count == The number of times a hashing function is applied to a password input. More iterations increase the computational effort required to generate or crack a hash, enhancing security.
Cost Factor == A parameter—used in algorithms like bcrypt—that exponentially increases the number of hashing rounds. For example, a cost factor of 12 means 2¹² (4,096) rounds, significantly raising the time and resources needed for each hash computation.
Hash Chaining == The process of feeding the output of one hash function directly into the next round, effectively compounding the hash strength across multiple iterations.
Embedded Salt & Iterations in Hashes
There are many hashing algorithms that produce hashes embedding both a sub-algorithm type, iteration count and a salt. A well-known example of this is bcrypt. Let’s take a look at a sample bcrypt hash and break down its individual components.
BCrypt Hash: $2y$10$SgVTvV0XOKTH/NqDyy0qc.rV.o6lOIJm9dqGI4iyAsKvr5TAlSBI.
$2y $10 $SgVTvV0XOKTH/NqDyy0qc. rV.o6lOIJm9dqGI4iyAsKvr5TAlSBI.
\_/ \_/ \_____________________/ \_____________________________/
Algorithm Cost Salt(always 22 Char) hash(always 31 Char)Phpass Hashes are another example of a format where the salt, iteration count, and final hash are all embedded within a single string. This self-contained structure allows password verification routines to extract everything they need directly from the stored hash.
Let’s take a look at the example hash below and break down the anatomy of a phpass hash.
PHPass Hash: $H$9HcJWK5yS94nXvcpo.w19AjiNb1XID.
$H$ 9 HcJWK5yS 94nXvcpo.w19AjiNb1XID.
\_/ \_/ \______/ \____________________/
Identifier Cost Salt (8 chars) Hash (22 chars)Hashing Algorithms Speed
When it comes to cracking hashes, the single most important attribute to consider is speed.
Take MD5, for example. One of its major flaws is that it’s incredibly fast. The faster a hashing algorithm is, the more guesses an attacker can attempt per second.
This guess rate is referred to as the hash rate, measured in hashes per second (H/s). A higher hash rate means faster brute-force attempts—and a significantly reduced time to crack weak passwords.
Hash Rate Chart
| Hash Rate | # Guesses Per-Second | |
| H/s | 1H/s = | 1 |
| KH/s | 1KH/s = | 1,000 |
| MH/s | 1MH/s = | 1,000,000 |
| GH/s | 1GH/s = | 1,000,000,000 |
Fast Hash Algorithms
Before we look at which hashing algorithms are intentionally slow, it’s important to understand just how fast something like MD5 really is.
Let’s establish a baseline: imagine we’re using Hashcat v6.2 on a system equipped with an NVIDIA RTX 2080 Ti GPU. With this setup, we can achieve a hash rate of approximately 50* billion MD5 guesses per second—that’s 50 GH/s*.
At that speed, brute-forcing weak or common passwords becomes trivial, which is exactly why fast hashing algorithms like MD5 are unsuitable for password storage.
Slow Hash Algorithms
Now let’s look at the opposite end of the hash rate spectrum. One of the most widely used slow and secure hashing algorithms today is bcrypt.
Bcrypt was specifically designed to resist brute-force attacks by being computationally expensive. This intentional slowness drastically limits how many guesses an attacker can attempt.
Using the same cracking setup—Hashcat v6.2 with an RTX 2080 Ti GPU—how does bcrypt perform? You’ll get around 41,000* guesses per second, or 41 KH/s*. That’s over a million times slower than MD5, making brute-force attacks far less feasible.
*These hash rates come from a Hashcat benchmark test. The actual hash rate will vary depending on many factors, such as attack mode, preprocessors, and rules.
Why Hash Rate Matters?
So why does hash rate change our approach to cracking passwords? With fast hashes, we can process an enormous number of guesses per second—often trillions—making brute-force attacks both feasible and effective. In these cases, we don’t need to waste time crafting clever strategies; sheer computational force is enough to break weak passwords in a matter of hours.
But when dealing with slow hashes—those deliberately designed to consume significant processing time—this brute-force method becomes impractical. Guessing trillions of passwords might take hundreds of years. In such scenarios, we need to rely on highly optimized, targeted attacks that prioritize password candidates with the highest statistical likelihood of success.
Section Key Terms
Hash Rate == The number of plaintext guesses per second that can be performed against a hash.
H/s == Hashes per second.
KH/s == Thousands of hashes per second
MH/s == Millions of hashes per second
GH/s == Billions of hashes per second
Wrap-up & Next Steps

Holy cow—that was a lot of information!
Like I mentioned at the top of this post, password cracking doesn’t sound all that complex at first glance—until you start digging into the details. And now you’ve seen just how deep the rabbit hole can go.
That said, if you’re just dabbling in password cracking as a one-off project, many of these technical nuances might seem like overkill. But if you’re planning to dive into password cracking as an ongoing research effort, understanding these foundational concepts is absolutely essential. Details like iteration counts, cost factors, and hash formats aren’t just academic—they directly affect the tools you use, the strategies you adopt, and ultimately, your success rate.
If you’re ready to move forward, the next blog post in this series will focus on the tools and tactics for brute-forcing passwords. Stay tuned.